[Data Structure] - Small intro to big O

Time execution varies between computers, so instead of talking about seconds or miliseconds, we talk about complexity to describe how long or how much space would an algorithm take to be executed.

Big O notations are essentials because having performant algorithms means having a fast-responding software. Who knows, you might even get a nice reward for optimizing an existing algorithm. Full story there.

Just a bit of maths to get a feeling on big O meaning. It actually describes the limiting behavior of a function when the argument tends to a value or infinity.
So, when you are saying O(N), you are actually saying, well my algorithm will take a number of steps that would be dominated by the linear function f(N) = N.
Just another example an we will dive into big O notation applied to computer science.

f(x) = cos(x) 
g(x) = x

Now the cosinus function is taking values only between [-1; 1], whatever x is. At the contrary, when x grows toward infinity, it’s taking larger values. So we can say that f is dominated by g, written:

f(x) = O(g(x))

Here I will mainly focus on time complexity. I may update later this article to add the space complexities too.

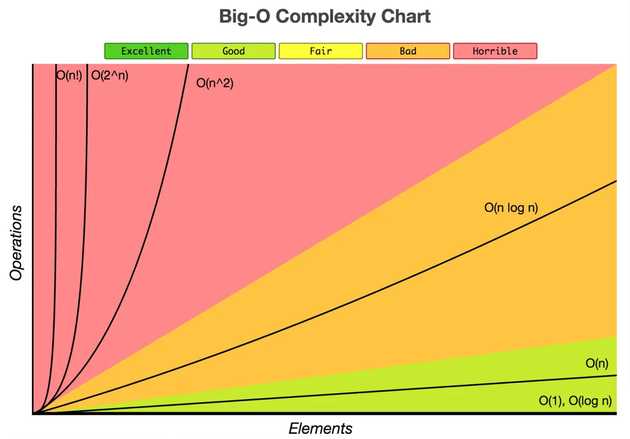This graphic sum up common complexities of algorithms

One last thing: Complexities are evaluatede in the best case, the worst case and on average. Usually, we take into account only the worst case scenario.

O(1)

This is the basic big O notation, it corresponds to one operation.

int number = 0;

O(N)

It correspond to N operations.
Let say we have an array of length N:

for (int i = 0; i < array.length; i++) {
   System.out.println(i);
}

The for loop iterates N times, thus this is a O(N) algorithm.

What would be the complexity of this algorithm ?
We have two arrays (array1 and array2):

for (int i = 0; i < array1.length; i++) {
   System.out.println(i);
}

for (int j = 0; j < array2.length; j++) {
   System.out.println(j);
}

Well, from the previous example, you would say that you have N operations for the array1 and N operations for the array2. Then the complexity would be O(2N).
One rule of big O notation is to drop constants because they don’t add any value to the global complexity, the complexity is then O(N).

Be careful! This reasoning is not entirely true. Here, we supposed that the two arrays were the same length (N) which is not necessarily the case!

Actually, the best thing to do at a job interview is to suppose that the two arrays have a different lengths, lets call them N and M. Now, the complexity of this algorithm is O(N + M).
Usually, the examiner will provide a information on N and M, like M < N. Thus, an other rule apply: only conserve the dominant term when additioning complexities.

Finally the complexity is O(N).

Drop the constants

Conserve the dominant term when additioning complexities

Exemple:

String[] names = {"Mike", "John", "Tim", "Mag"};

for (int i = 0; i < names.length; i++) {
   System.out.println(names[i]);
}

The complexity is O(4) because our array is of length 4. Generally we will say it’s a O(1) complexity.

int sumNumber(int N) {
   int sum = 0;
   
   for (int i = 0; i < N; i++) {
      sum += i;
   }

   return sum;
}

In this case we iterate N times, the complexity is O(N). Notice that the initialization of sum variable or the incrementation are O(1) operations, but since we are doing N operations we end up with O(N) time complexity.

O(log(N))

Often when in a problem a number of elements get halved each iteration, it probably is a O(log(N)) runtime.
Let’s say we are searching for a number in an array. The algorithm is:
Take the middle element, if it is the number we are looking for, return.
If the element < number, search in the new array on the left. Otherwise search on the right.

Exemple:

Starting with 32 elements, after the first step only 16 remains, then 8 …

N = 32
N = 16
N = 8
N = 4
N = 2
N = 1

corresponds to:

N = 2⁵
N = 2⁴
N = 2³
N = 2²
N = 2¹
N = 2⁰

For any N, we are going to have: N = 2^k, the question is how do we find k, the number of steps ?

N = 2^k ⇒ log₂(N) = k

That where comes from the O(log(N)) complexity.

Details:
N = 2^k
⇒ ln(N) = k*ln(2)
⇔ ln(N)/ln(2) = k and log₂(N) = ln(N)/ln(2)
thus, N = 2^k ⇒ log₂(N) = k

O(N²)

When loops are imbricated, the runtimes are multiplied:

int doStuff(int N) {
   for (int i = 0; i < N; i++) {
      for (int j = 0; j < N; j++) {
         System.out.println(i + j);
      }
   }
}

We do N println for each element, N times, the complexity is O(N * N) = O(N²).

Generally, if we have two arrays with A and B lengths respectively:

int doStuff(int[] A, int[] B) {
   for (int i = 0; i < N; i++) {
      for (int j = 0; j < N; j++) {
         System.out.println(i + j);
      }
   }
}

We do B println of A elements, thus the complexity is O(A * B).

O(2^N)

This kind of complexity concerns the algorithms performing two operations simultaneously, in a recursive function that makes two recursive calls for instance.
Generally, if a recursive function makes more than one call, the complexity is O(branches^depth).

int f(int i) {
   if (n <= 1) {
      return 1;
   }

   return f(n-1) + f(n-1);
}

Two branches, with a depth of N: O(2^N). Draw a graph for an exemple, with N=3 or N=4.
At each step, the function is called twice more than the previous one.

O(N!)

As you may have guessed, it performs N! operation at runtime.
Avoid this kind of living hell.
Bogosort

To conclude - The key takeaways

• Drop the constants
• Drop the non-dominants terms
• Add complexities when operations are performed one after another
• Multiply complexities when for a number of operations, each steps require an other amount of operations
• Let me point you to this nice repository with more exercises if you want to practice

Any remarks ?

Make a pull request or open an issue!
Don’t know how to do it ? Check out this very well explained tutorial